这篇帖子给出一些多层线圈的“高频特性”的仿真结果。“高频”是指最高上百MHz。仿真中主要关注的是线圈“电感”和“等效串联电阻”随频率的变化，特别是第一个自谐振点的频率。因为仿真的速度很慢，所以这篇帖子以连载的形式发出。
一. 2024年3月26日的结果：
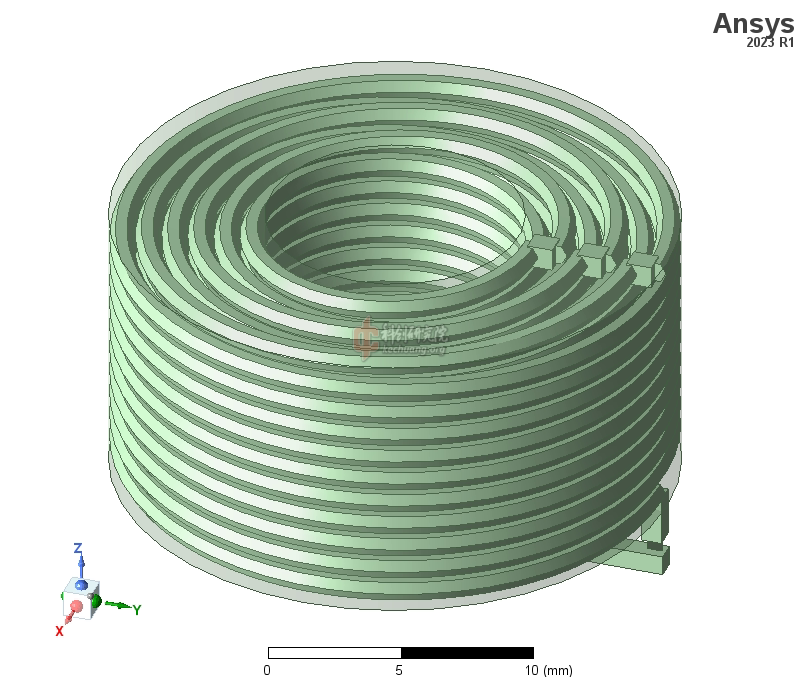
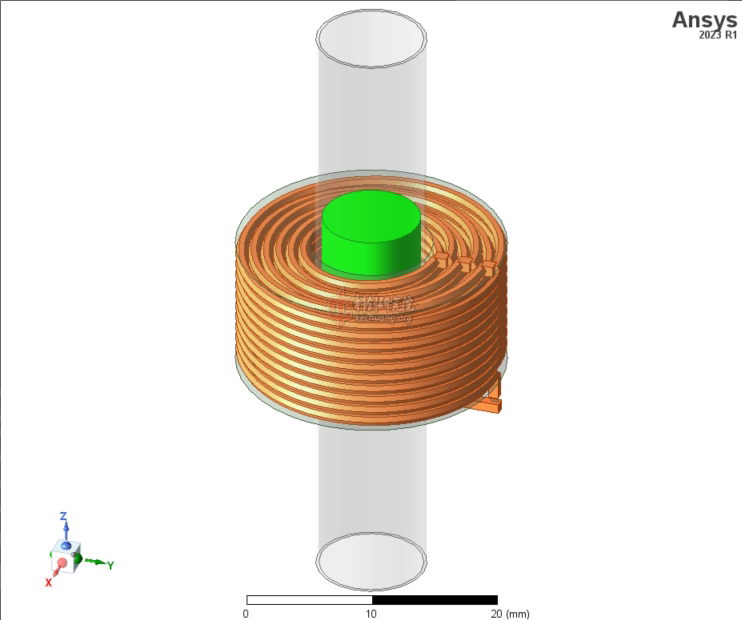
仿真模型如下图。这是一个矩形截面的多层空芯圆柱形线圈。线圈线径是0.9mm，材质为铜，仿真中将“圆形”的导线近似成“六/八边形”。线间距是0.1mm。每层有10匝，一共有6层，下图中各层用不同颜色显示。每层都是螺旋形，层间互联是通过加一个小方块实现的。线圈内径是10mm，外径22mm，长10mm。仿真中的馈源是一个集总端口，阻抗50Ohm，它通过一小截线和线圈的两端相连。
一般来说，这种线圈会用Ansys Maxwell这种准静磁学软件进行仿真。但是这篇帖子里，仿真用Ansys HFSS进行。这是因为“准静磁学”中，“位移电流”被认为是零，即不存在电容。而我们想要观察的自谐振特性，显然和电容高度相关。因此不能用准静磁仿真，必须用电磁仿真。
线圈的网格如下图。因为线圈的结构是“曲面+细线”，必须划分非常多的网格，所以仿真速度很慢，内存占用也比较多。这层楼里的出现的三个仿真结果，在i7-9750H的笔记本上，一共需要仿真大约10个小时，最多占用内存30 GB左右。
这层楼里一共有三个仿真结果：
结果1中使用较大的空气盒子，使用八边形导线
结果2中使用较小的空气盒子，使用六边形导线
结果3中使用较小的空气盒子，使用六边形导线，且勾选了solve inside。
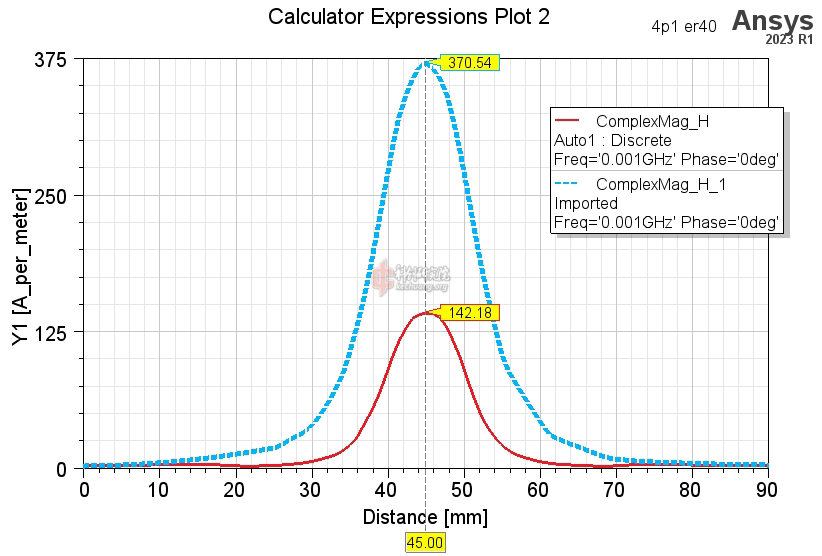
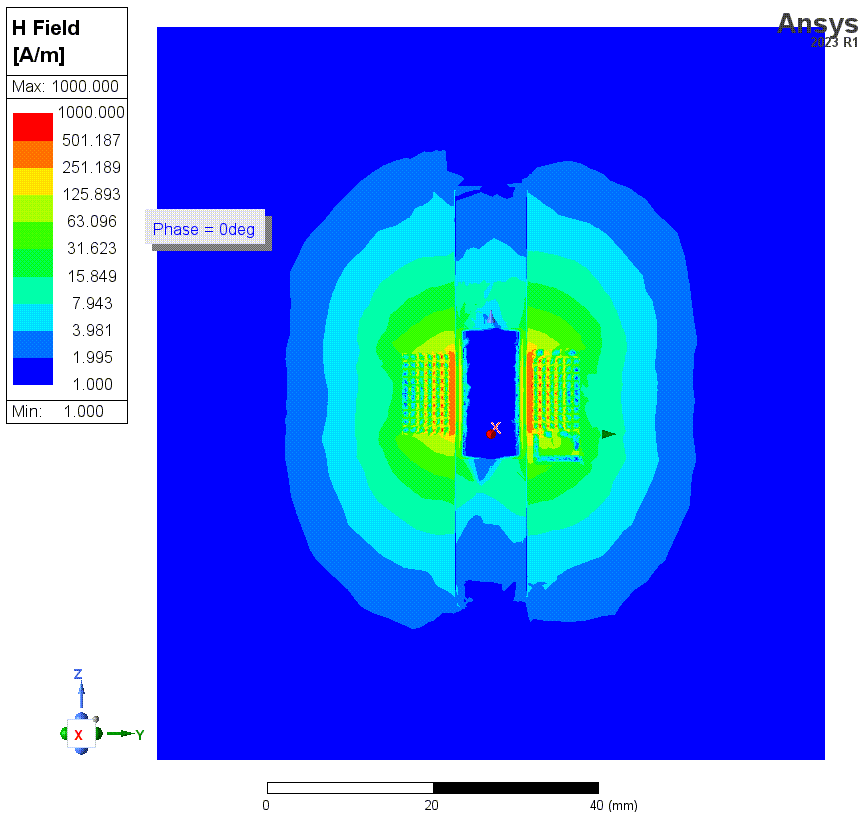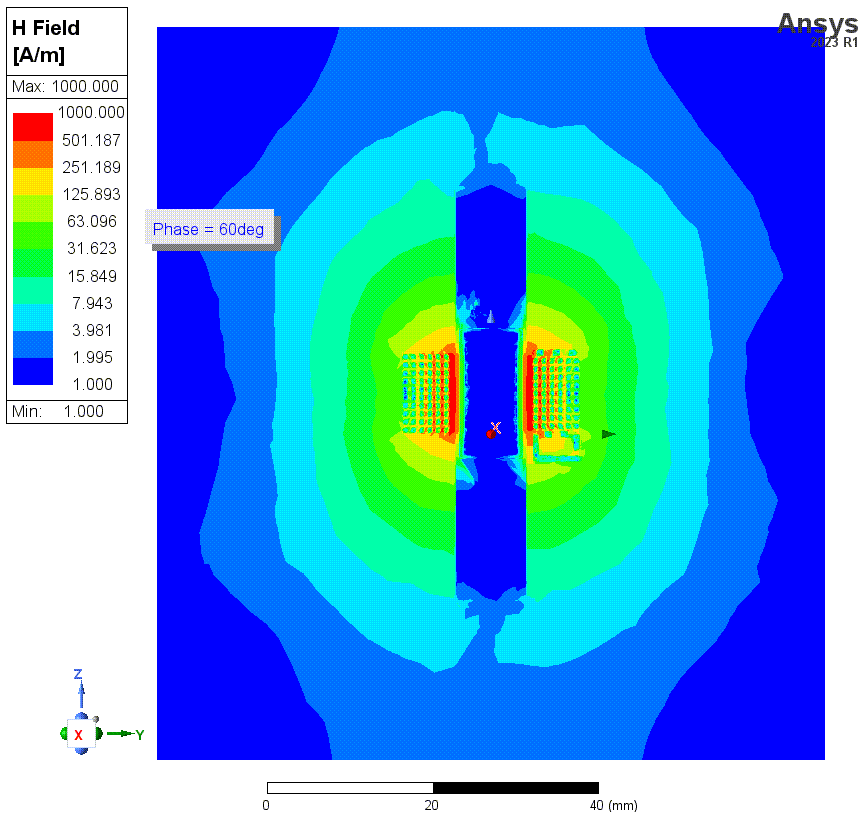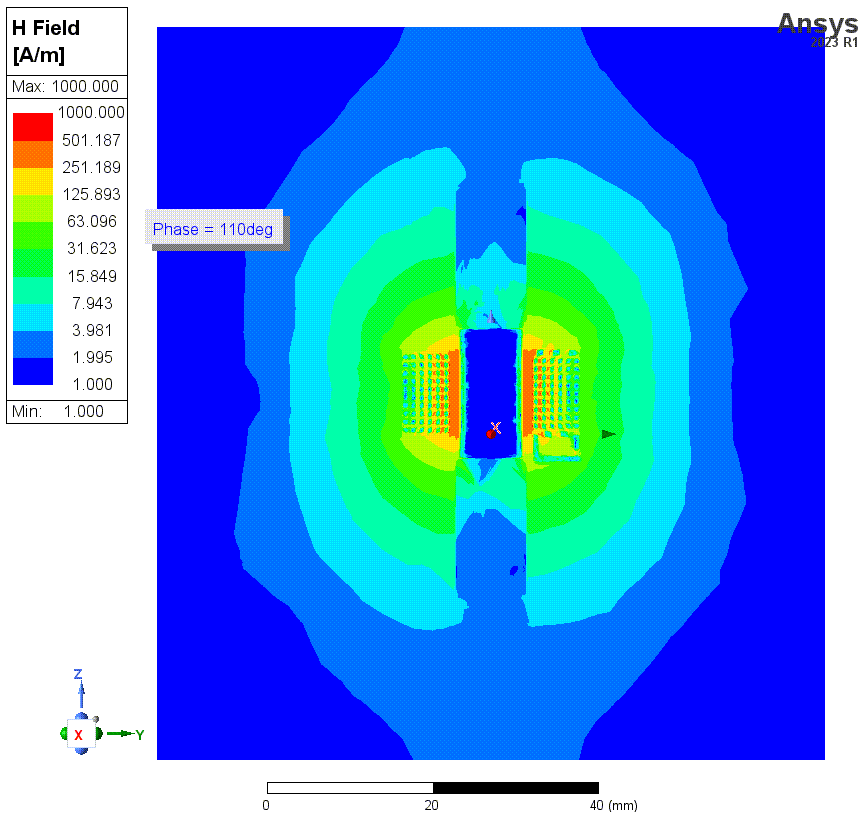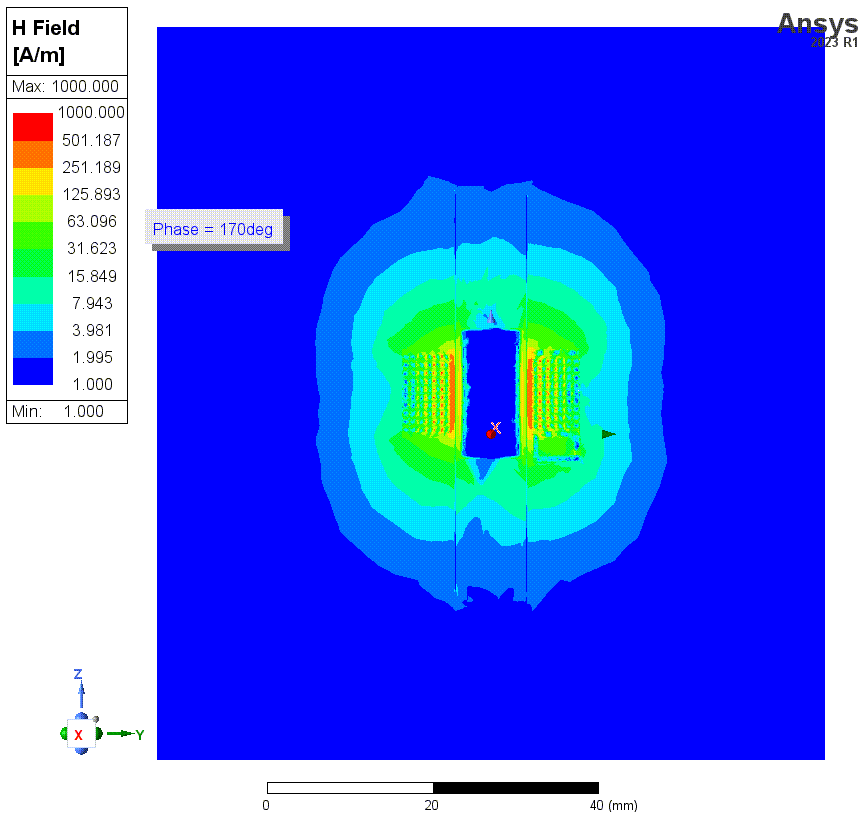
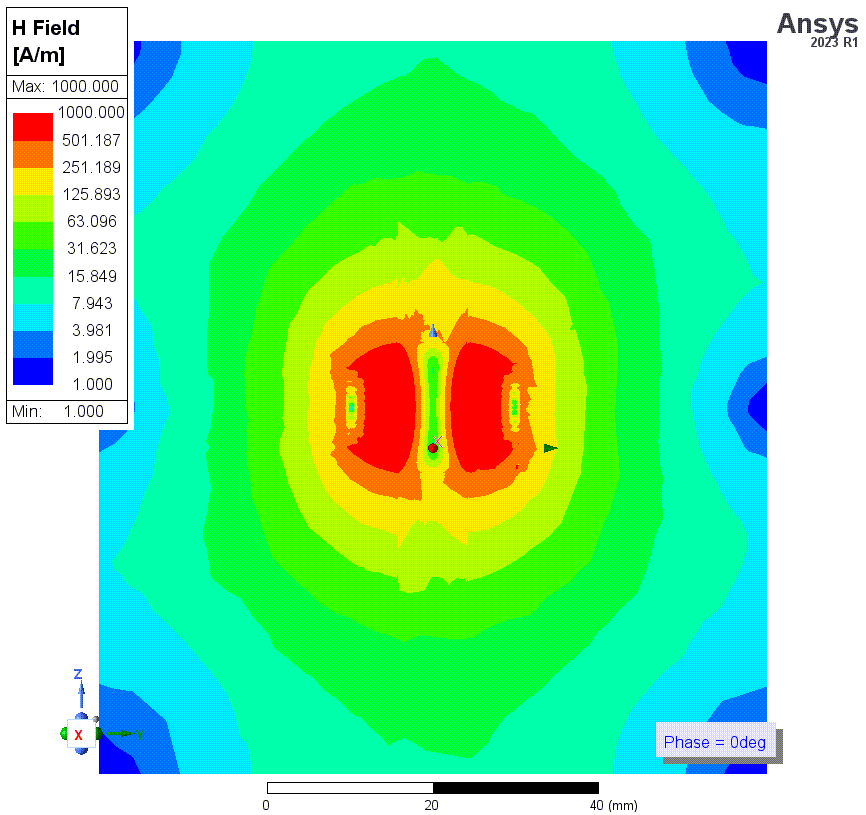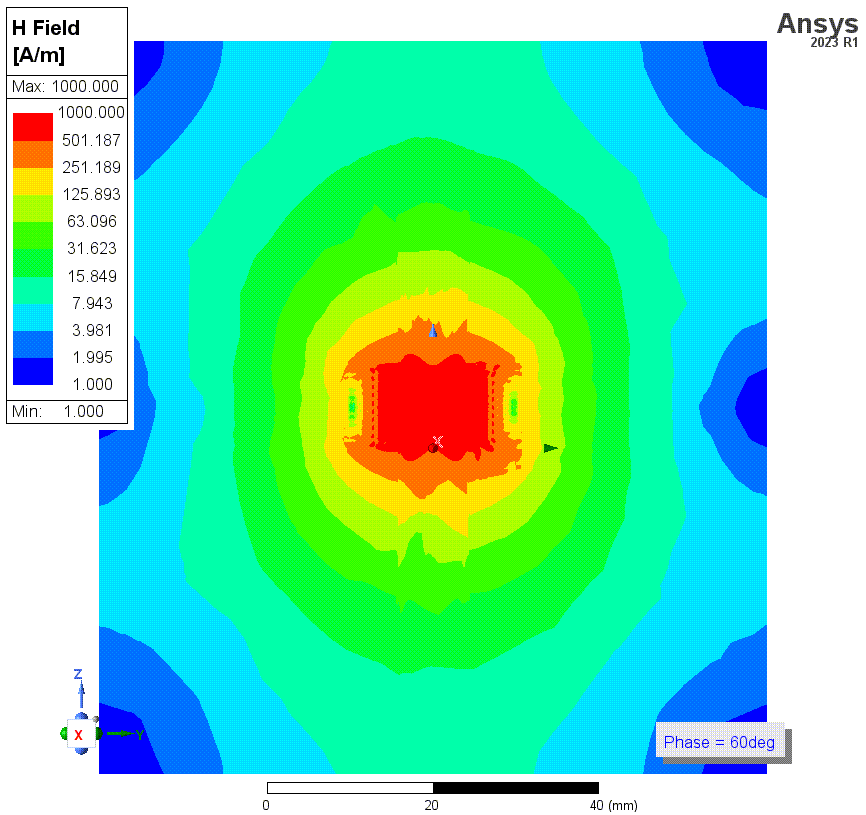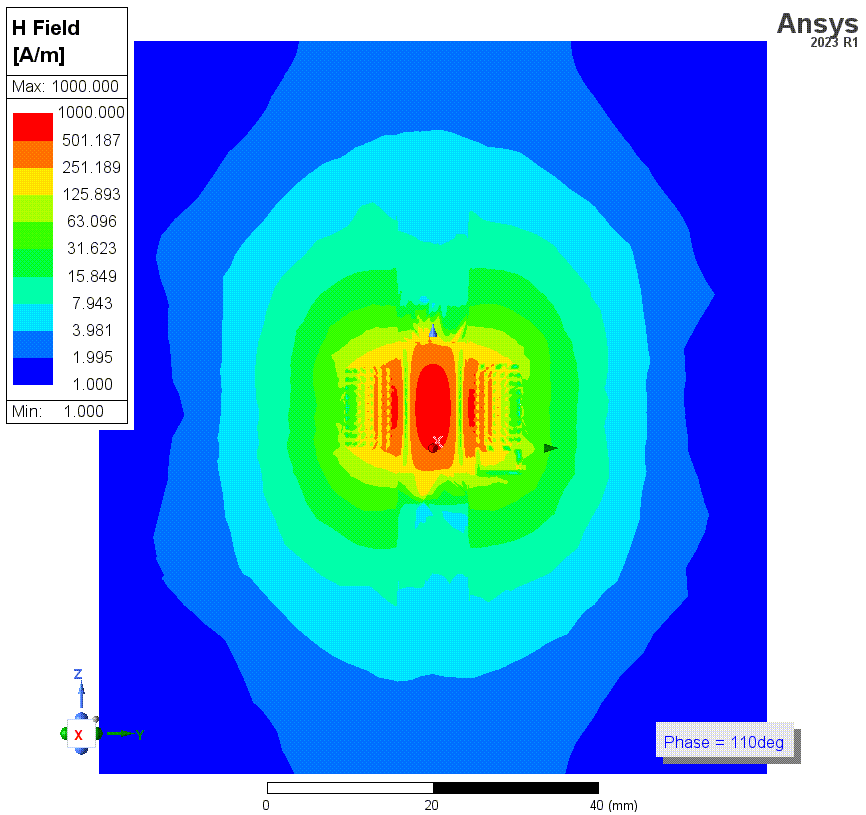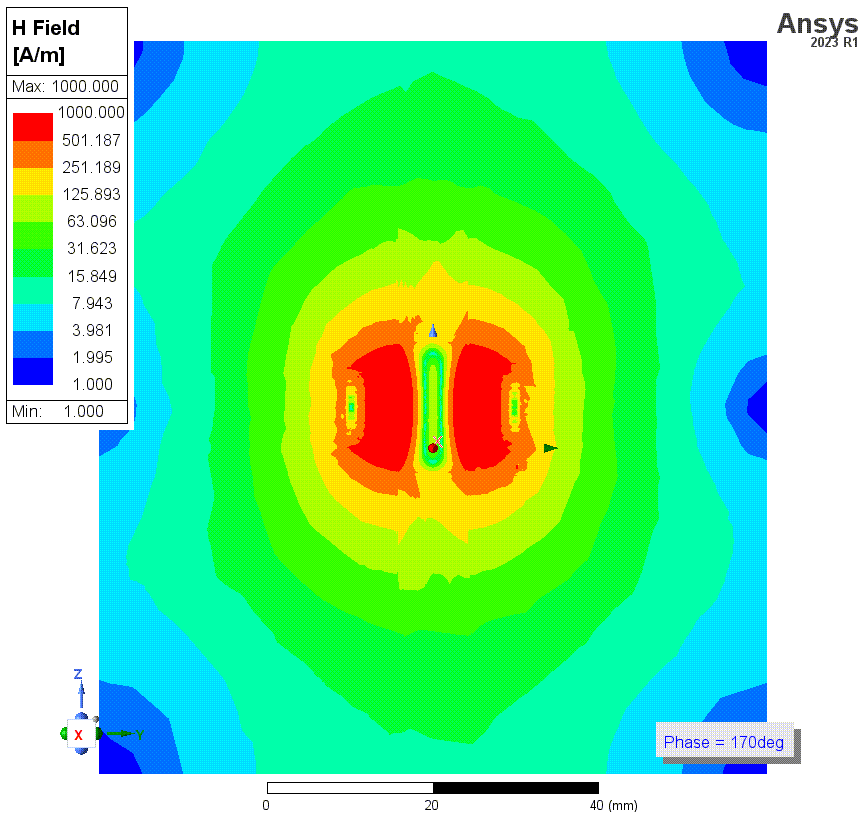
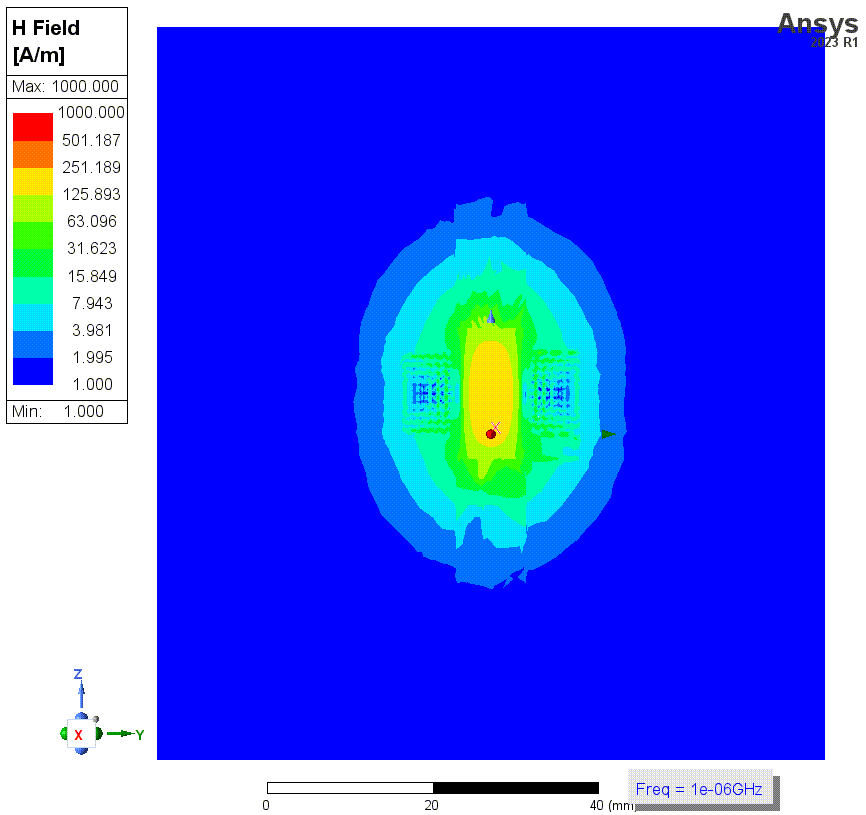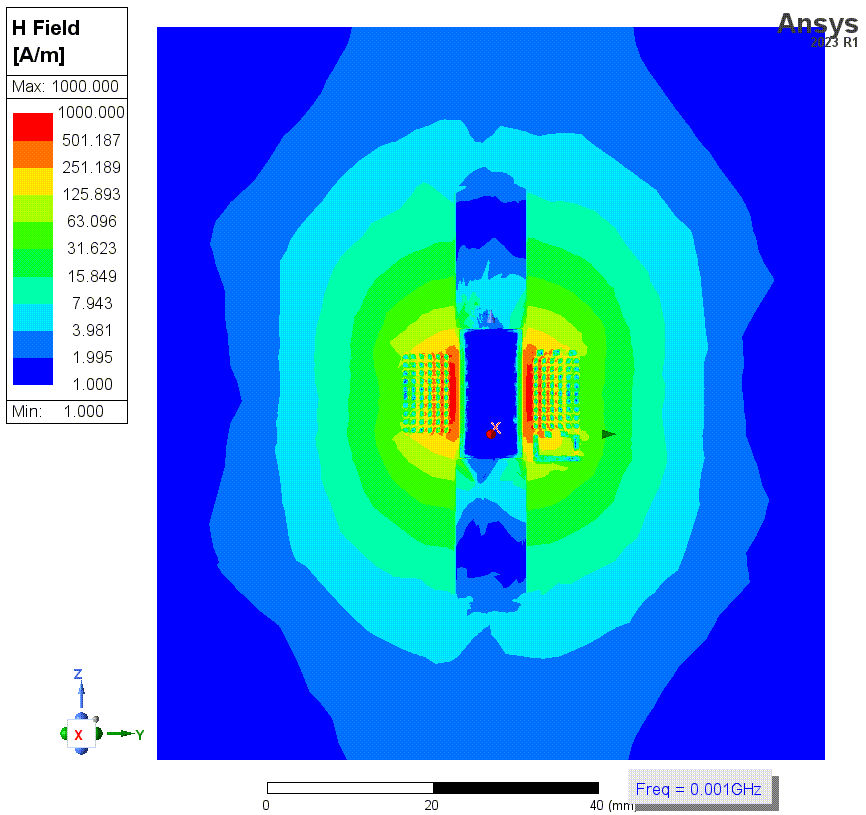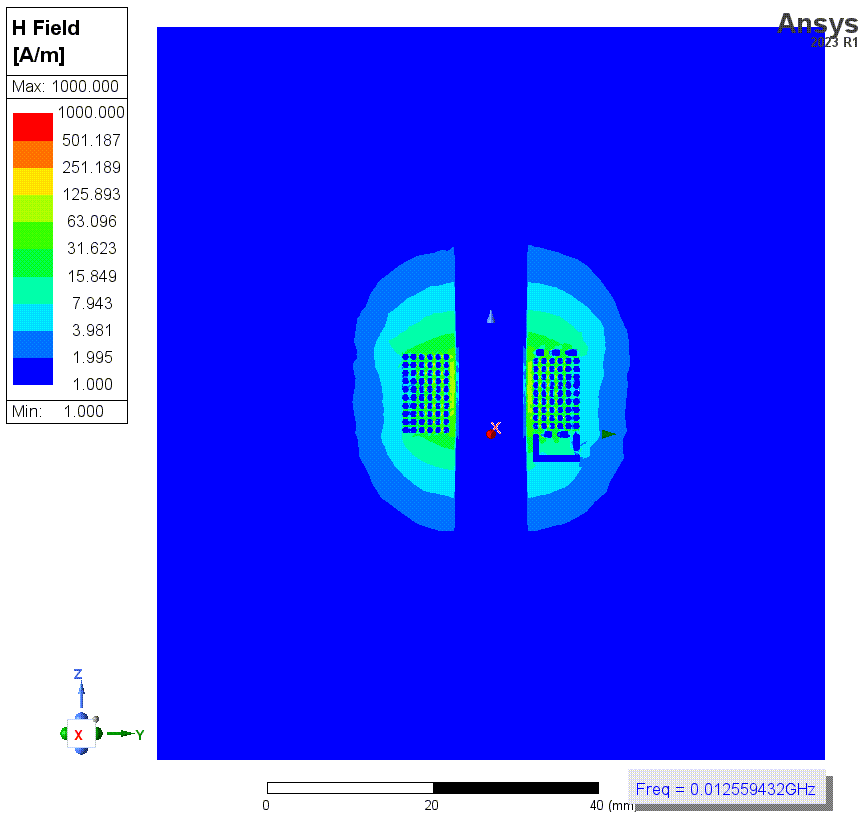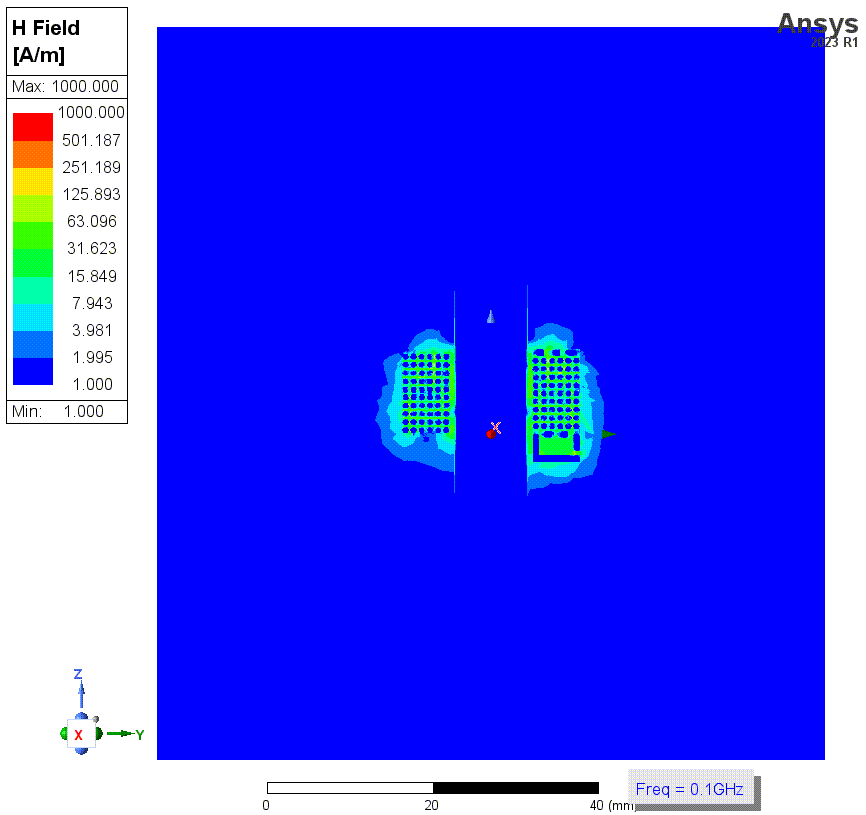
结果2和3的仿真的磁场强度如下。一共有四张图，仿真频率均为1MHz，这些图使用了对数标尺。HFSS中，金属材料默认是不solve inside的，即假设电流只在金属表面流动，金属内部磁场为零。前两张图（结果2）就是在这种条件下的结果。这种假设在HFSS的常规应用条件下，比如几GHz的频率，是正确的。但是这里我们的频率最低会仿到1kHz，此时这个假设就很错误了。因为这种低频下，磁场可以充分渗透到导线内部。后两张图的仿真中（结果3）纠正了这个错误。
上两张图是没有勾选solve inside时（结果2）的磁场强度，第二张是线圈部分的细节图
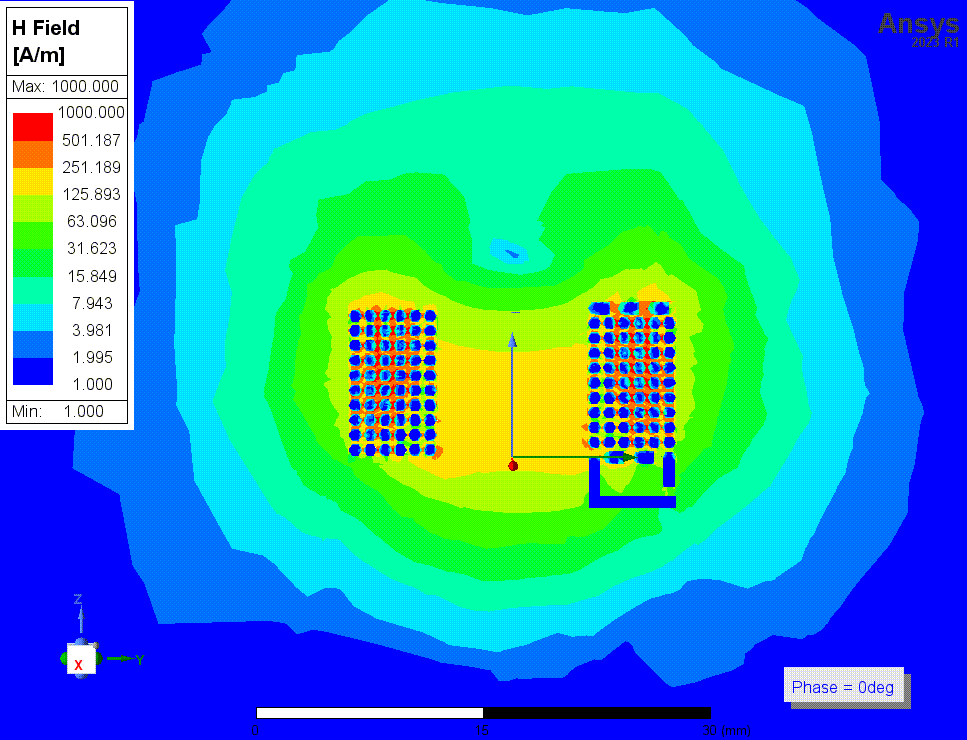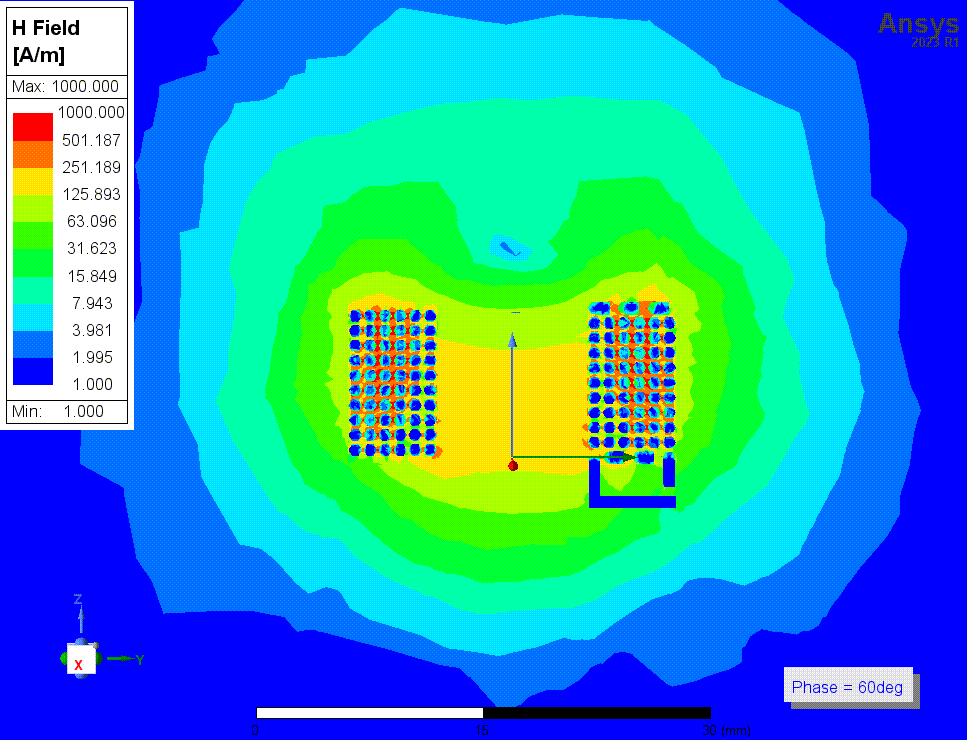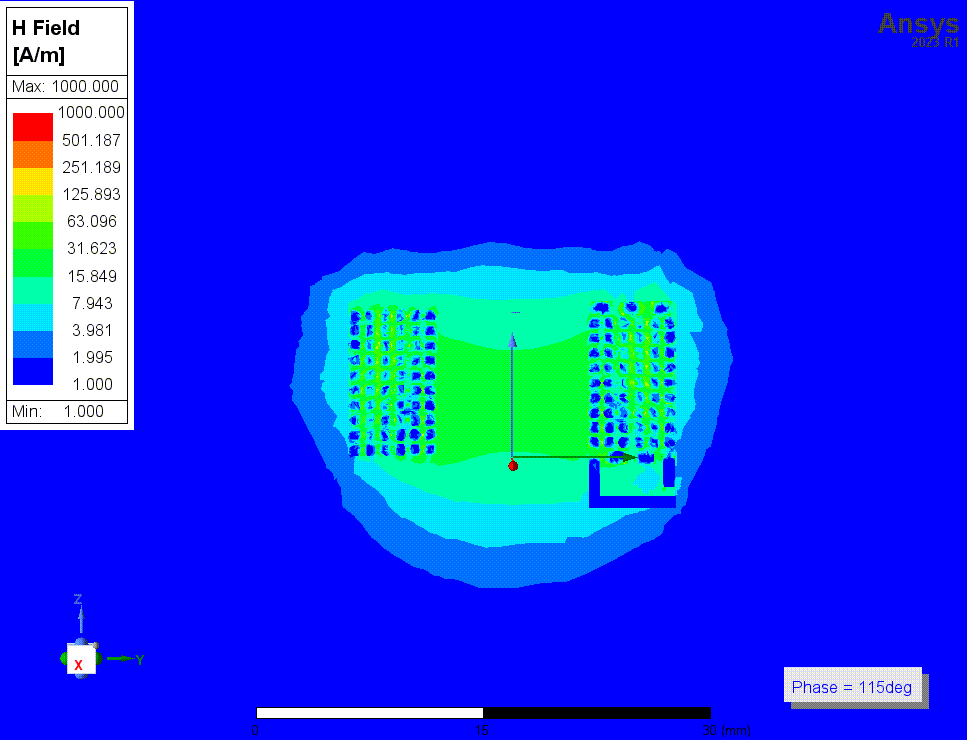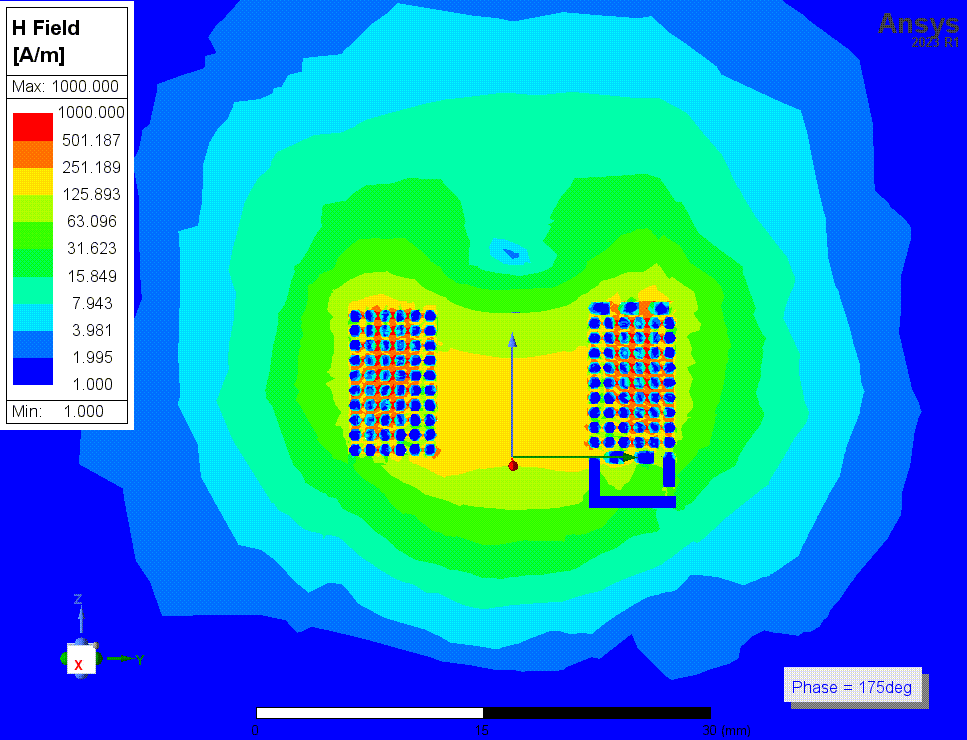
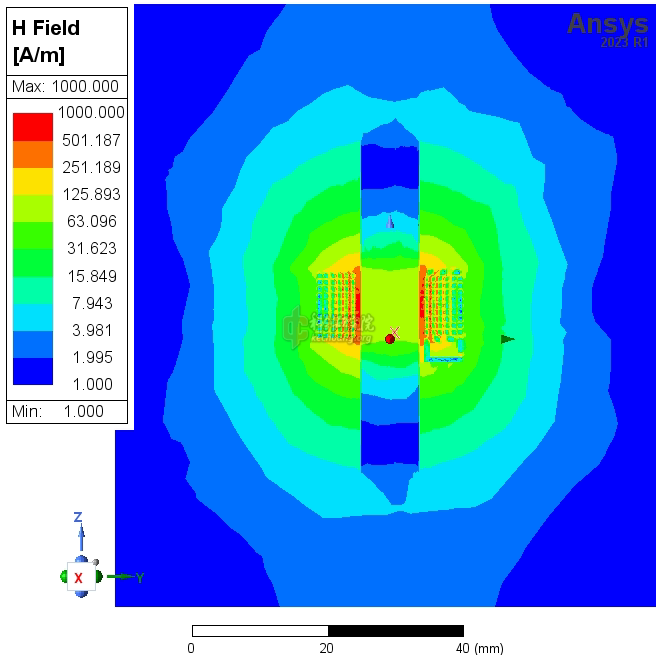
上两张图是勾选了solve inside时（结果3）的磁场强度
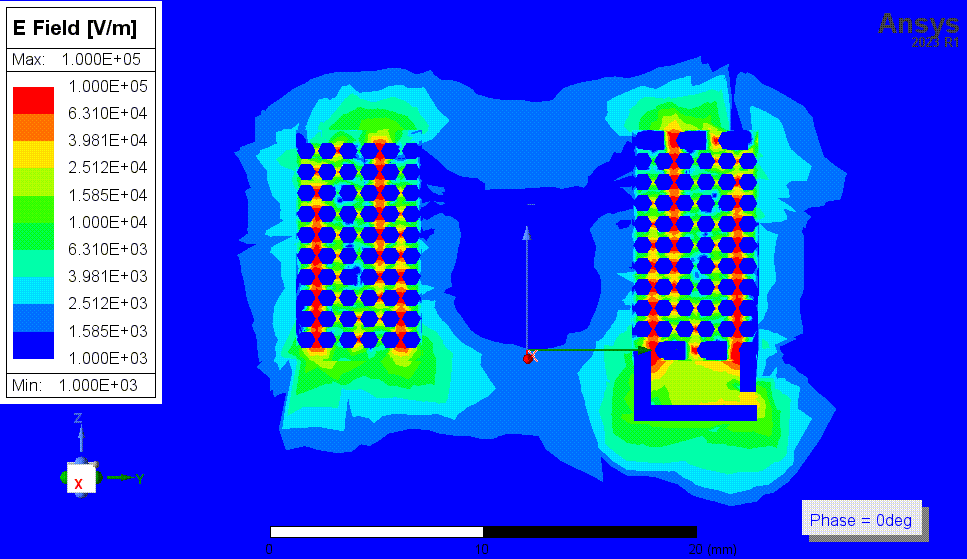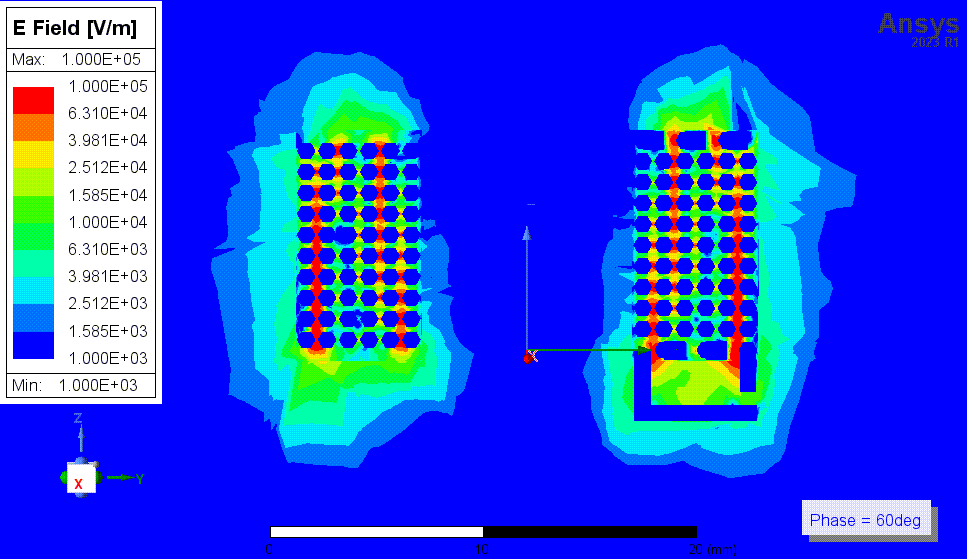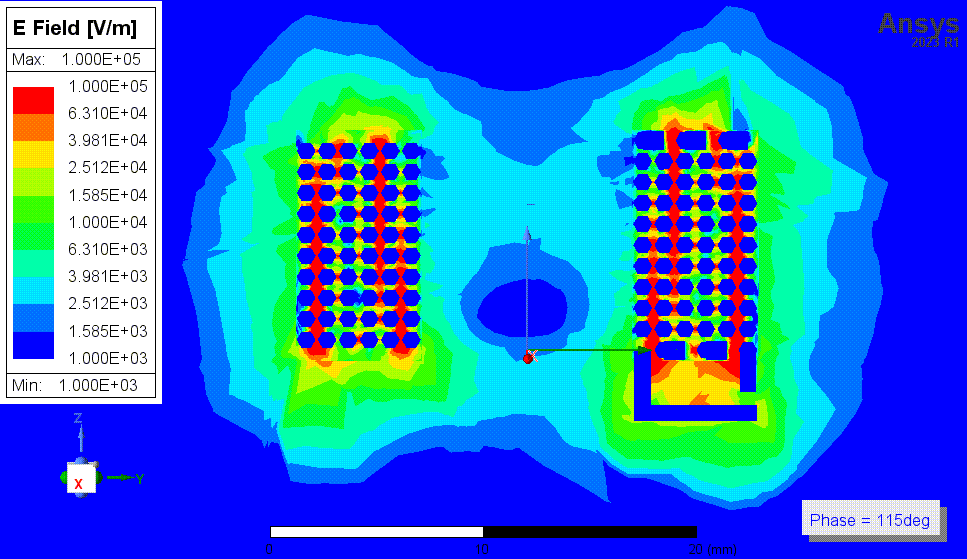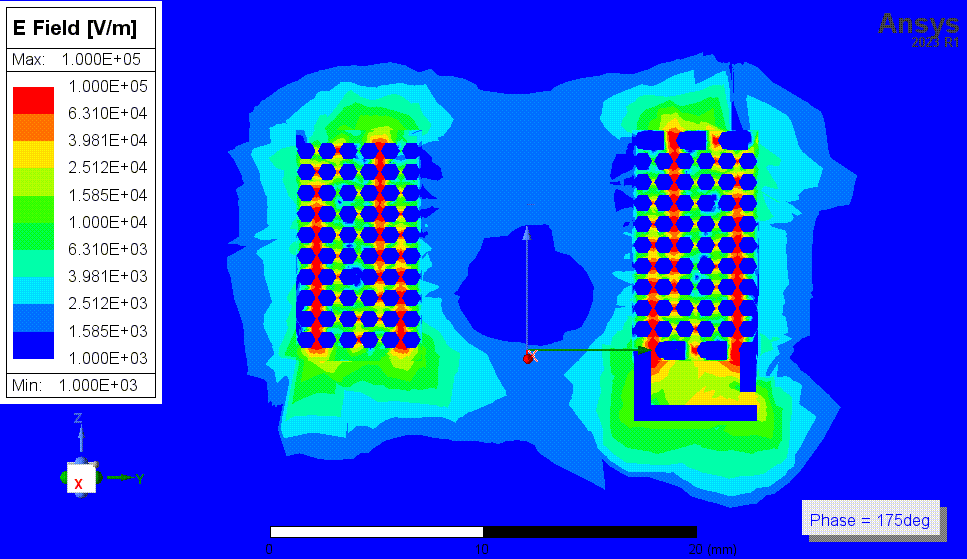
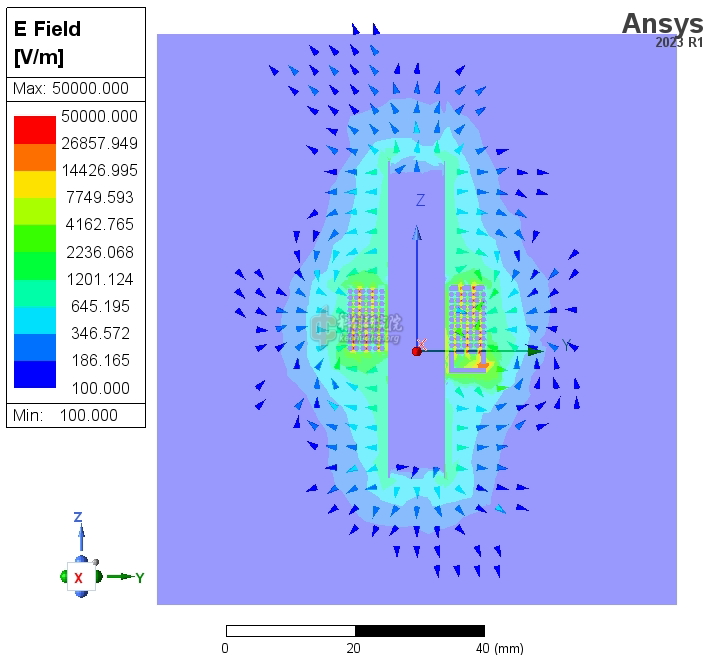
下两张图是结果3中，1MHz时的磁场动图，以及16MHz时（自谐振频率附近）的电场动图。我还看了其他频率时的电场和磁场图，我没有看出自谐振点附近有什么特别的现象，场分布基本没有变化。
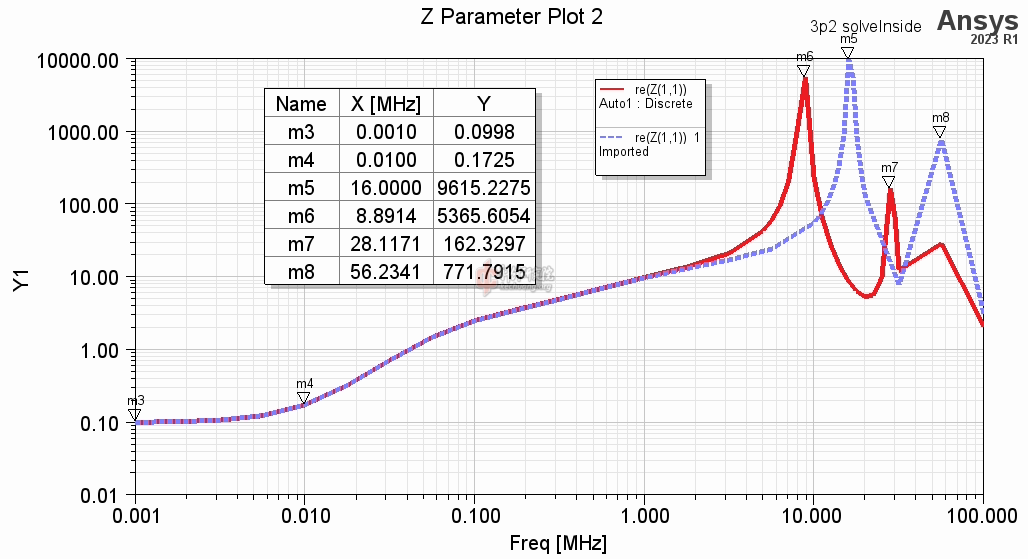
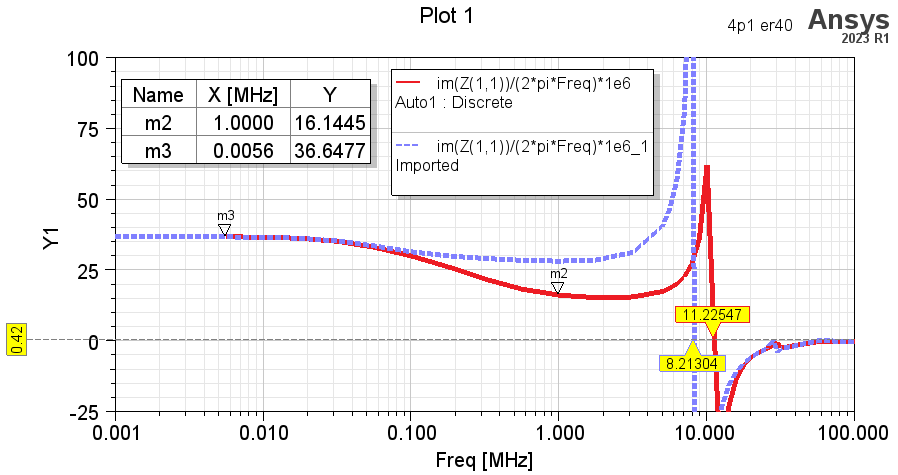
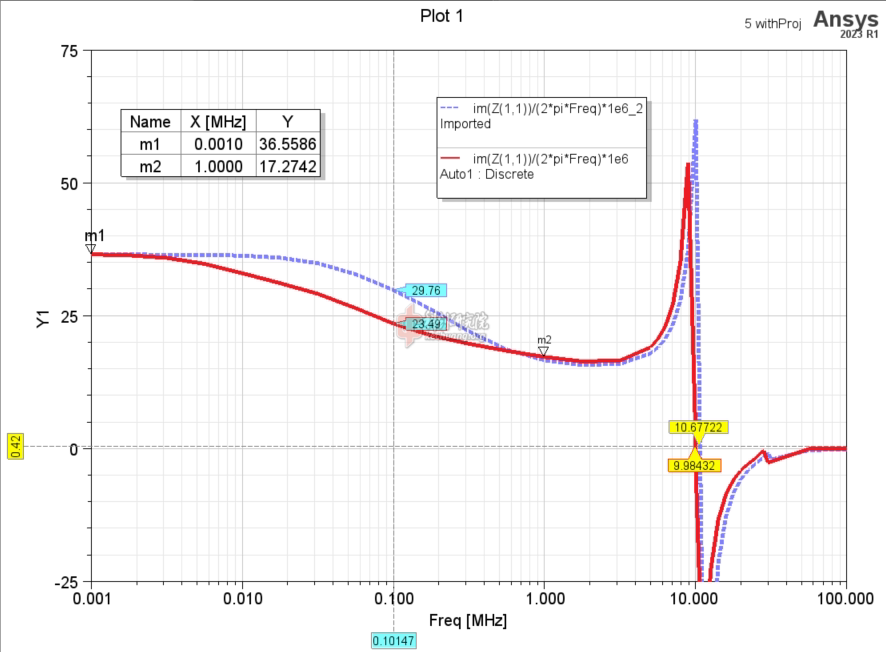
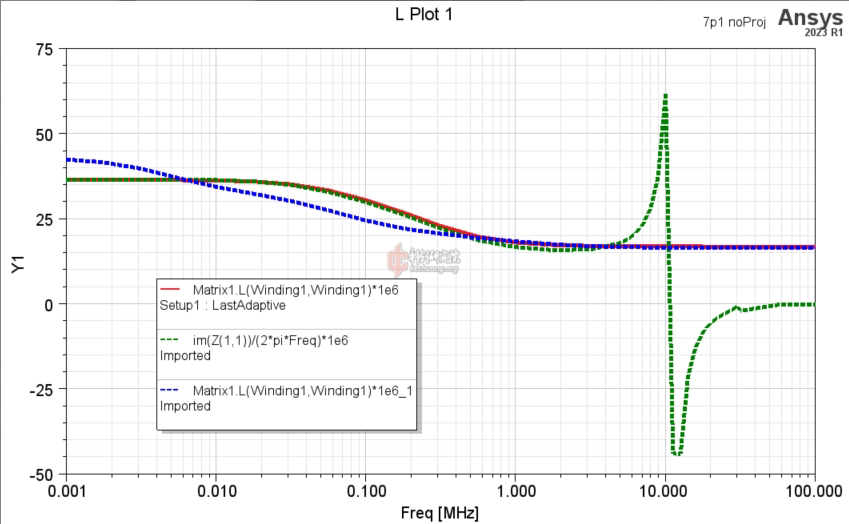
仿真的电感如下图。横轴是频率，纵轴是电感量（单位是uH）。绿色虚线是结果1，红色线是结果2，蓝色线是结果3。可以看出，结果1和结果2的差别不大，说明使用小空气盒子和六边形线问题不大。结果2和3的自谐振点在16.7MHz左右，比结果1的频率略高一点。这是比较合理的，毕竟六边形之间的电容，显然会比八边形的更小。低频时，结果3和结果1，2的差别很大，主要体现在低频时结果3的电感明显更小。
作为对比，使用常见的hacoilgun模拟器计算这个线圈的电感和电阻，结果如下图。结果3的电感，在低频下和hacoilgun的极为接近。
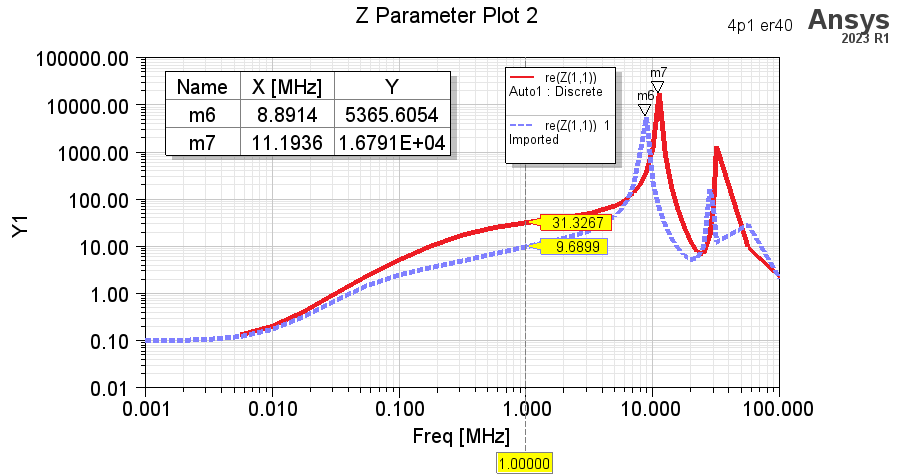
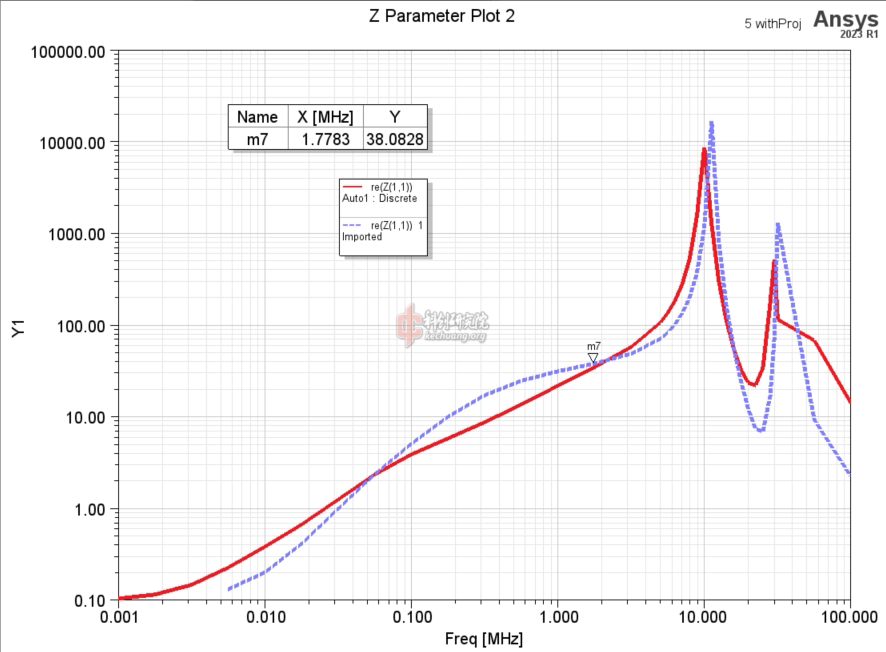
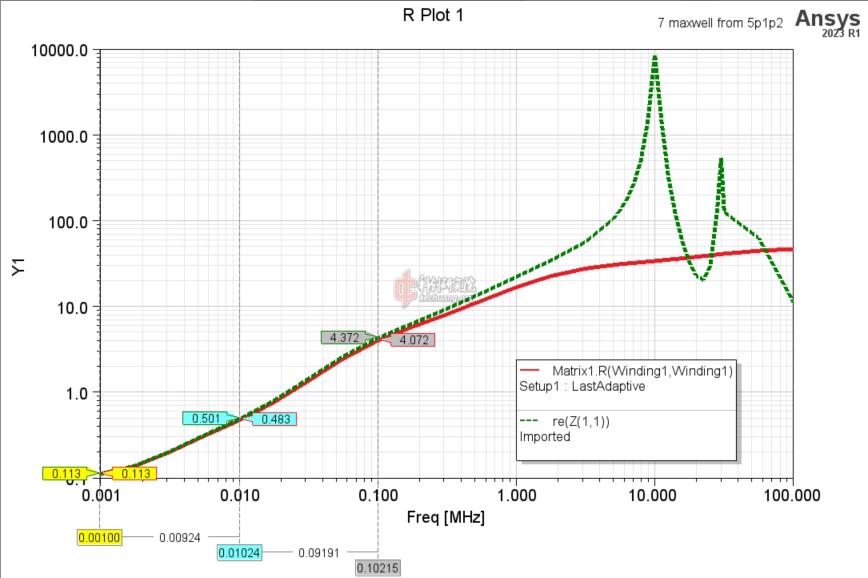
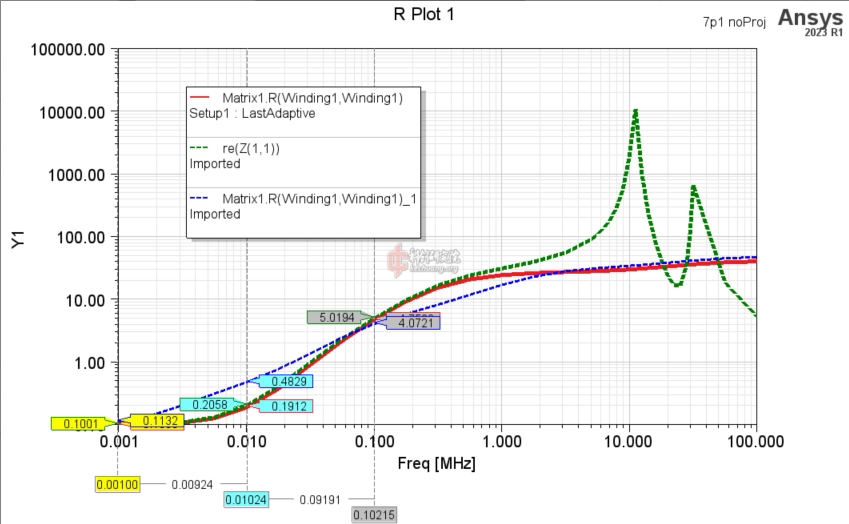
仿真的电阻如下图。纵轴单位是欧姆。其中结果3在1kHz时的电阻是99.8mOhm，而且电阻率的上升发生在更高频率处，看起来都更加合理。
结果3看起来更正确一些，不过代价也很大，主要体现在仿真速度上。结果2只需要不到2个小时，而结果3需要七个多小时。
仿真文件如下：
[修改于 9 个月前 - 2024/03/26 16:58:36]
二. 2024年3月28日的结果
在3月26日的仿真中，只考虑了金属部分，没有考虑到介质的影响。
这次更新了模型，给线圈加上了介质。下图中透明色的部分是介质，它是一个空芯圆柱形。介电常数为4。
仿真的电感量和电阻如下图：
其中，虚线是3月26日的结果3的曲线，实线是这次仿真的曲线。自谐振频率降低到了8.2MHz，大约是没有介质时的一半。这比较合理，因为介电常数从1增加到4，对应着电容量增加到原来的四倍，谐振频率也就应该变为原来的一半。
另外注意到，从电阻-频率曲线上看，28.1MHz处，有一个比较弱的谐振点。这应该是3倍频处的谐振。这个频率下的电场和磁场比较有特点，如下图。可以看到电场在第三和第四层之间异常的弱，而磁场似乎出现了“定向性”，下方比上方略强。
仿真模型如下：
三. 2024年3月29日的结果
在3月28日的模型的基础上，在线圈中间添加一根不锈钢管，如下图。不锈钢管内径8.5mm，外径9mm，长50mm，电导率1.1e6 S/m。
仿真的电感和电阻如下图。虚线是3月28日的结果，实线是这次的结果。这次的高频电感量有所下降，自谐振频率从8.2MHz提升到了11.2MHz。高频的电阻还有所增加。
仿真的电场与磁场图如下，频率是1MHz。电场图中，可以看到不锈钢管上出现了一些感应电场。磁场图中，可以看到不锈钢管对磁场起到了屏蔽的效果。但是其内部的磁场只是减弱了，不是完全没有了。
下图是线圈轴线上的磁场强度。虚线是3月28日的结果，实线是这次添加不锈钢管之后的效果。可以看到，磁场强度从371 A/m下降到了142 A/m。
仿真模型如下：
四. 2024年4月1日结果
之前的仿真速度太慢，内存占用太大，所以这次仿真在3月29日的基础上，修改了一些仿真设置，来提高速度，降低内存占用。具体修改了三个地方，如下图。将网格剖分的精细程度下调了一格，从“偏右两格”调整为“偏右一格”。将基函数从first order调整为mixed order。将求解器从direct solver调整为iterative solver，并且将relative residual从默认的1e-6调整为1e-4。
进行如上调整之后，仿真耗时从8小时53分，下降到了4小时46分。内存占用从43GB下降到29GB。下面第一张图是3月29日的结果，第二张图是这次的结果。
仿真的电感和电阻曲线如下图，虚线是3月29日的结果，实线是这次的结果。两次仿真的结果有细微差别，但是可以接受。
四. 2024年4月1日结果之前的仿真速度太慢，内存占用太大，所以这次仿真在3月29日的基础上，修改...
上述结果都是在一台i7-9750H + 64GB内存的笔记本上运行的。
另外，我还在一台性能更强的台式机上运行了完全一致的仿真。台式机的配置是i9-10900K + 128GB内存。然而出乎意料的是，台式机上的仿真速度并没有快出许多。笔记本上耗时4小时46分的仿真，台式机上也需要3小时51分，仅快了24%。而根据XXXXXXXXXXXXXXXX 上的跑分结果，i9-10900K应该是 i7-9750H 的两倍才对。
五. 2024年4月5日的结果
今天首次出现了无法理解的现象。
这次仿真在4月1日的基础上，修改模型，在线圈内添加一个金属圆柱，如下图。圆柱的直径为8mm，长16mm。其电导率为 6315730 S/m，与常见钢材类似。其相对磁导率被设置为 1。
仿真的1MHz处的磁场随相位的变化如下图
10kHz时的磁场随相位的变化如下
仿真的不同频率的磁场如下图（相位保持在90度）
仿真的电感和电阻如下图
在低频下（几百kHz以下）的表现是可以理解的。此时线圈的电感量变低，这是因为添加金属圆柱之后，线圈内部的导体变多了。电阻（损耗）则是在几十kHz以下时变大，在几十kHz以上时变小，这是因为新加入的金属的“导电性”比原本的不锈钢更强。
然而在几百kHz以上的频率，出现了无法理解的现象。此时加入金属圆柱之后的电感量，反而比之前的略微大了一点。同时在2MHz以上，加入金属圆柱之后的电阻又重新超过了之前的值。自谐振点也略微向低频偏移了一些。
这种“导体越多电感越大”的现象，我还无法理解为何会发生。
六. 2024年4月7日的结果
在4月5日的结果的基础上，调整了“金属圆柱”的相对磁导率，将其改为 2.0 和 10.0，分别进行仿真。
仿真得到的电感和电阻如下图。其中，蓝色虚线是不添加金属圆柱时的结果（4月1日的结果）。绿色是虚线是添加了金属圆柱，且其相对磁导率为 1.0 时的结果（4月5日）。红色实线和橙色实线，分别是相对磁导率为 2.0 和 10.0 时的结果。在不同的相对磁导率下，在1MHz以上的频率，均出现了“导体越多电感越大”的现象。
七. 2024年4月8日的结果
在4月7日中相对磁导率 ur = 2.0 的结果的基础上，修改金属圆柱的位置，令其沿z轴方向平移。对平移-18mm到0mm的情况进行仿真，模型如下图
仅对 100kHz 到 1MHz 范围内的电感进行仿真，仿真结果如下。在相对高频处，比如1MHz，依然有比较明显的“导体越多电感越大”的现象。
2024年6月21日更新，补充电阻结果：
之前在10mm骨架上绕了一个约160匝的多层线圈，脱模之后测电感136uH；将一根6*35mm的Q235定位销塞入线圈内部，测电感141uH。
2024年6月19日
改用maxwell仿真同样的模型。maxwell是一个“准静磁”仿真软件，它在进行磁场仿真时认为电容为零。
仿真所用模型与“2024年4月7日”的模型在机械结构上基本一致，“金属圆柱”的相对磁导率设置为 2。
模型的主要区别是馈电方式不同，hfss里用的是阻抗 50ohm 的 lump port。maxwell里用的是 coilTerminal，电流恒定为1A。这个对于仿真电阻电感没有影响，但是会对磁场图有影响。hfss里端口阻抗恒定，线圈阻抗随频率升高而变大，所以频率越高，磁场越弱。maxwell里端口电流恒定，所以磁场幅度随频率也基本不变。
仿真的电感和电阻如下，实线是这次仿真的结果，虚线是“2024年4月7日”的结果。可以看到使用maxwell仿真时没有出现自谐振特性，低频时的结果和hfss吻合良好，频率越高差别越大。
10kHz时磁场动图如下：
100kHz时的磁场动图如下：
1MHz时的磁场动图如下：
仿真的速度和内存占用如下：
2024年6月21日
在“2024年6月19日”的基础上去掉金属柱。红色实线是这次的结果，绿色虚线是使用hfss仿真同样模型时的结果，蓝色虚线是2024年6月19日的结果（磁导率为2的金属柱）。
2024年6月21日 - 2
尝试仿真线径更细的线圈，如下图。模型中，线径为0.4mm，线与线之间有0.1mm的缝隙，即相邻导线中心距0.5mm。每层20匝，一共12层。该线圈外轮廓与前文所述的线圈一致，但是每层匝数和层数都变成了两倍。
不幸的是，这个模型无法仿真：即使在128GB内存的电脑上，也会报 out of memory 的错误
仿真文件如下：
