我核验了一下,首先,81010 中的算式应该是错了,正确的公式不是
而应当是
推导如下
带入
有
如果带入这个公式,计算出的效率是35.3%。问题在于这个计算结果仍然和帖子中的40.8%有差距。
由于帖子中的计算不满足81010 中的前提,我们可以考虑一下瞬时效率而不是全局效率。
有瞬时效率等于:
可以看出,速度越快,瞬时效率越高,本贴的模拟在高速段电流小,低速段要更大一些,理论效率应当略低于使用恒流的效率。我百思不得其解,然后我重新运行了一下我之前写的代码,给出的效率并不是40.8%!!!
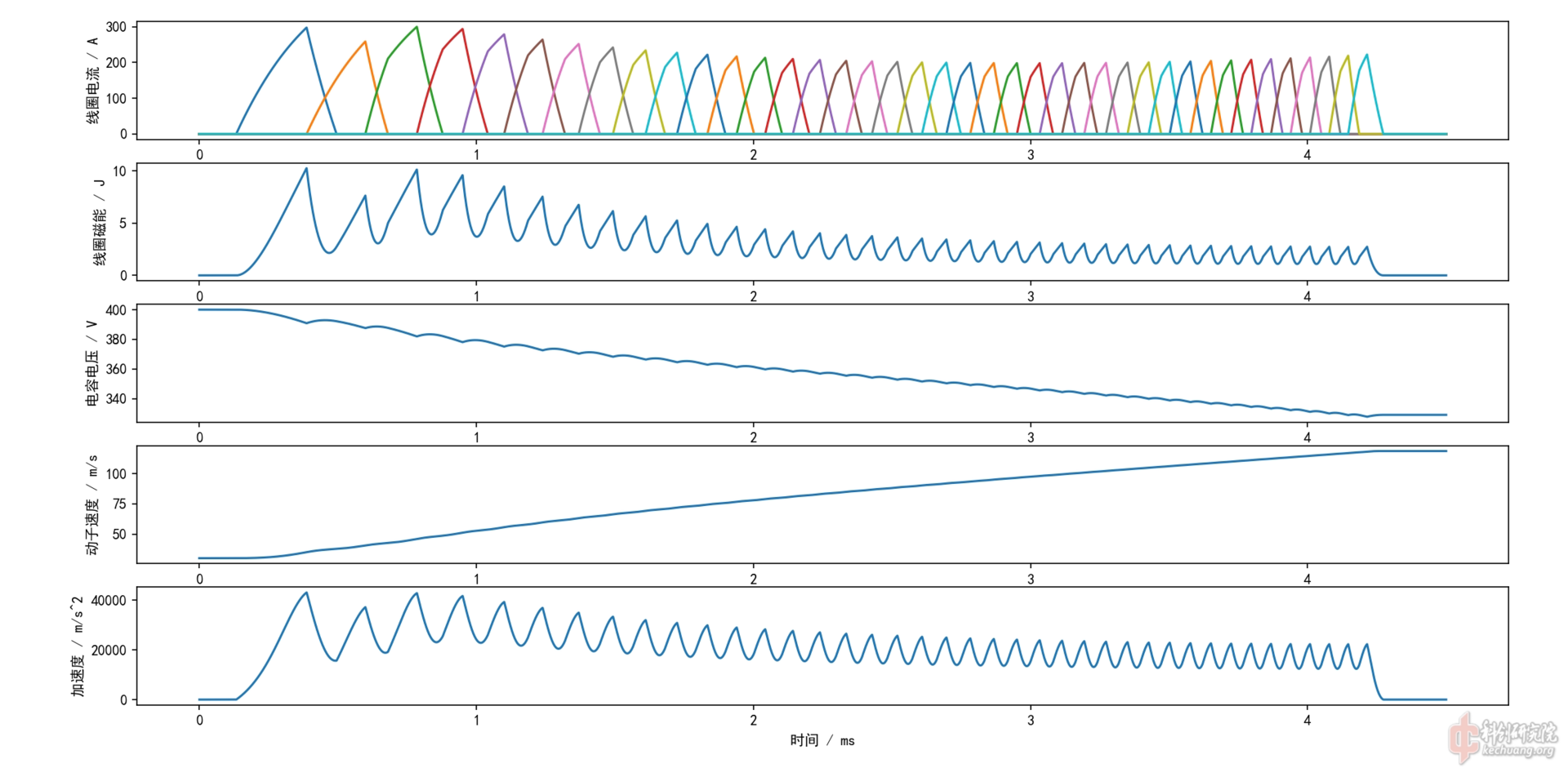
![image.png]()
效率应当是34.4%。非常费解到底是出了什么错误导致当时计算出了40.8%的效率