首先对于第一个实例, 基于几何布朗运动的股票价格模型, 进行阐述和解读. 笔者是2018年入市的新股民, 作为新鲜的韭菜总有一些不着边际的想法, 笔者并非是金融数学专业的学生, 但的确数年来都没能跳出经管类的大圈, 所以本着一贯的对于数学领域的叶公好龙, 以及对于金钱的贪婪, 笔者尝试通过ChatGPT对金融数学, 尤其是股票/期货市场的价格模型进行入门的学习. 而首当其冲的数学方法, 就是在统计物理和混沌/复杂系统中也有普遍应用的随机微分方程. 这一方法对于甚至没有系统学习过理科高数的笔者来说可以说是一窍不通的, 但通过与GPT4之间循序渐进的学习交流, 窥见美感并不难做到.

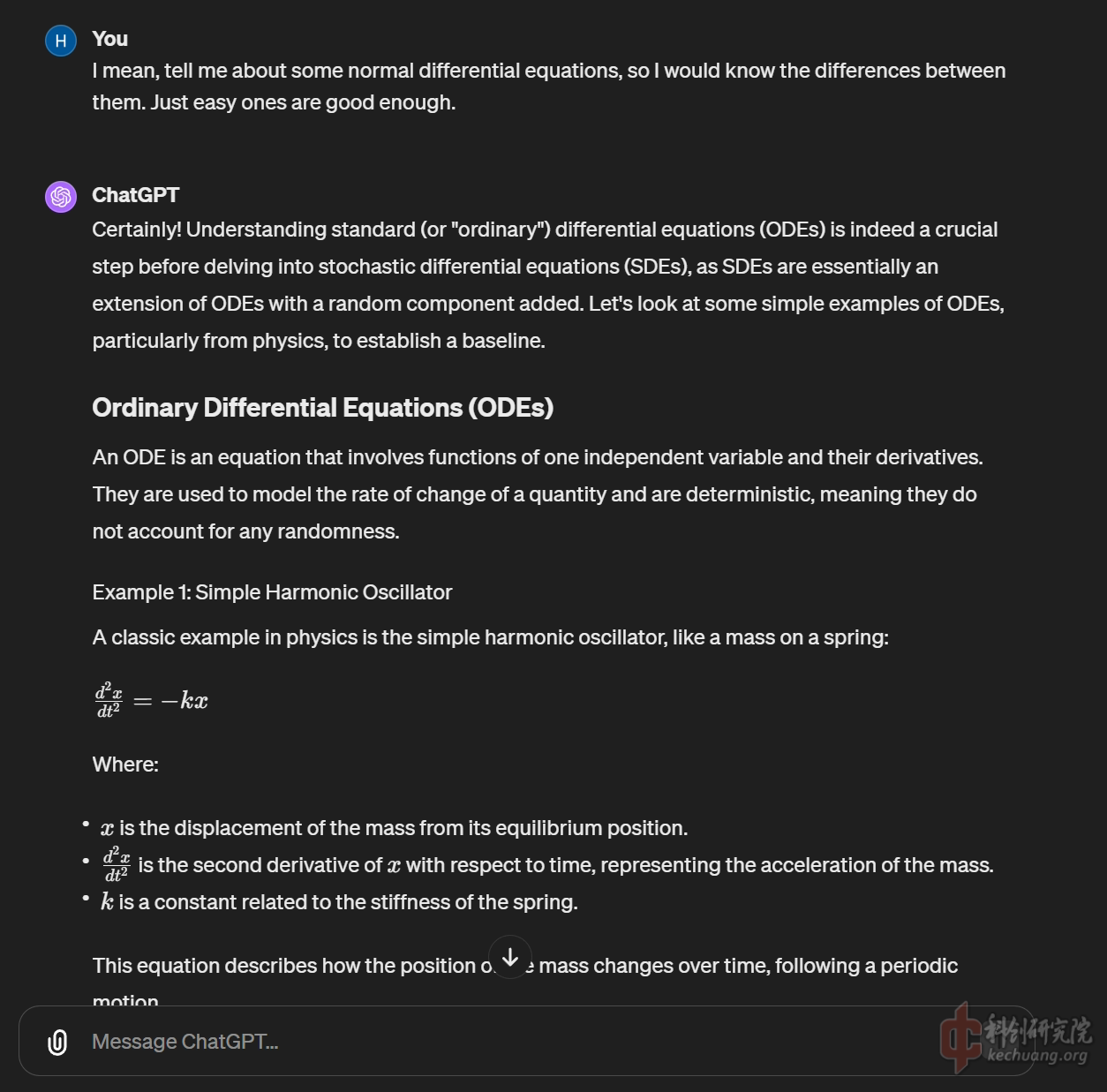
一些复习工作, 通过对弹簧振子简谐运动进行复习, 捡起为数不多的关于常微分方程的知识, 可以发现, GPT4依然会犯一些小错误,比如在此方程中忽略了振子的质量m.

通过卖关子的方式指出它存在问题, GPT4可以做到很好的自我纠错, 敏锐发现了缺少质量参数.

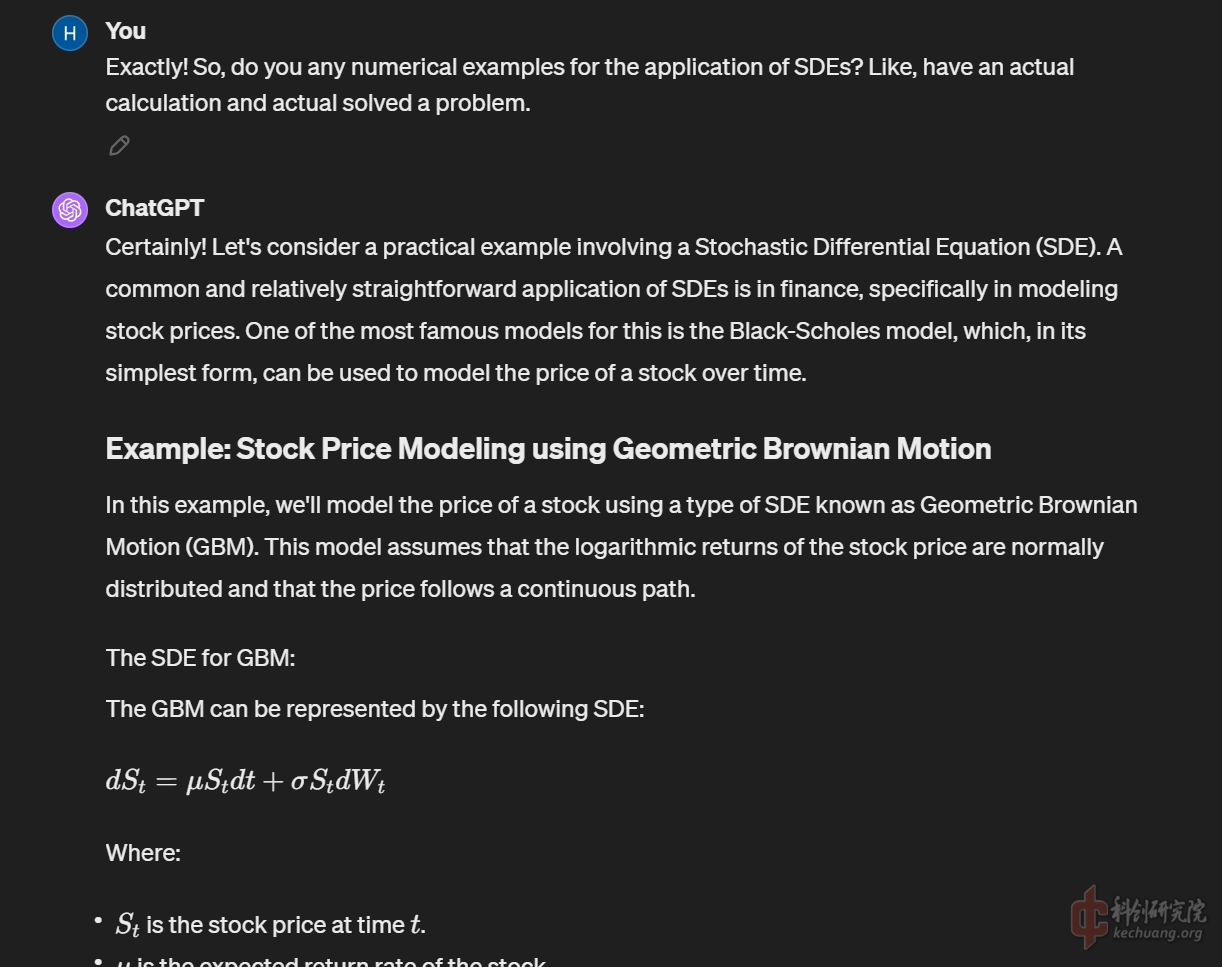
切入正题, 询问有关Stochastic Differential Equation的知识, 很巧, GPT4.0第一反应就是基于几何布朗运动的股价模型, 看来它的训练库里关于这种数学方法的部分还是金融数学领域的文献更多一些.

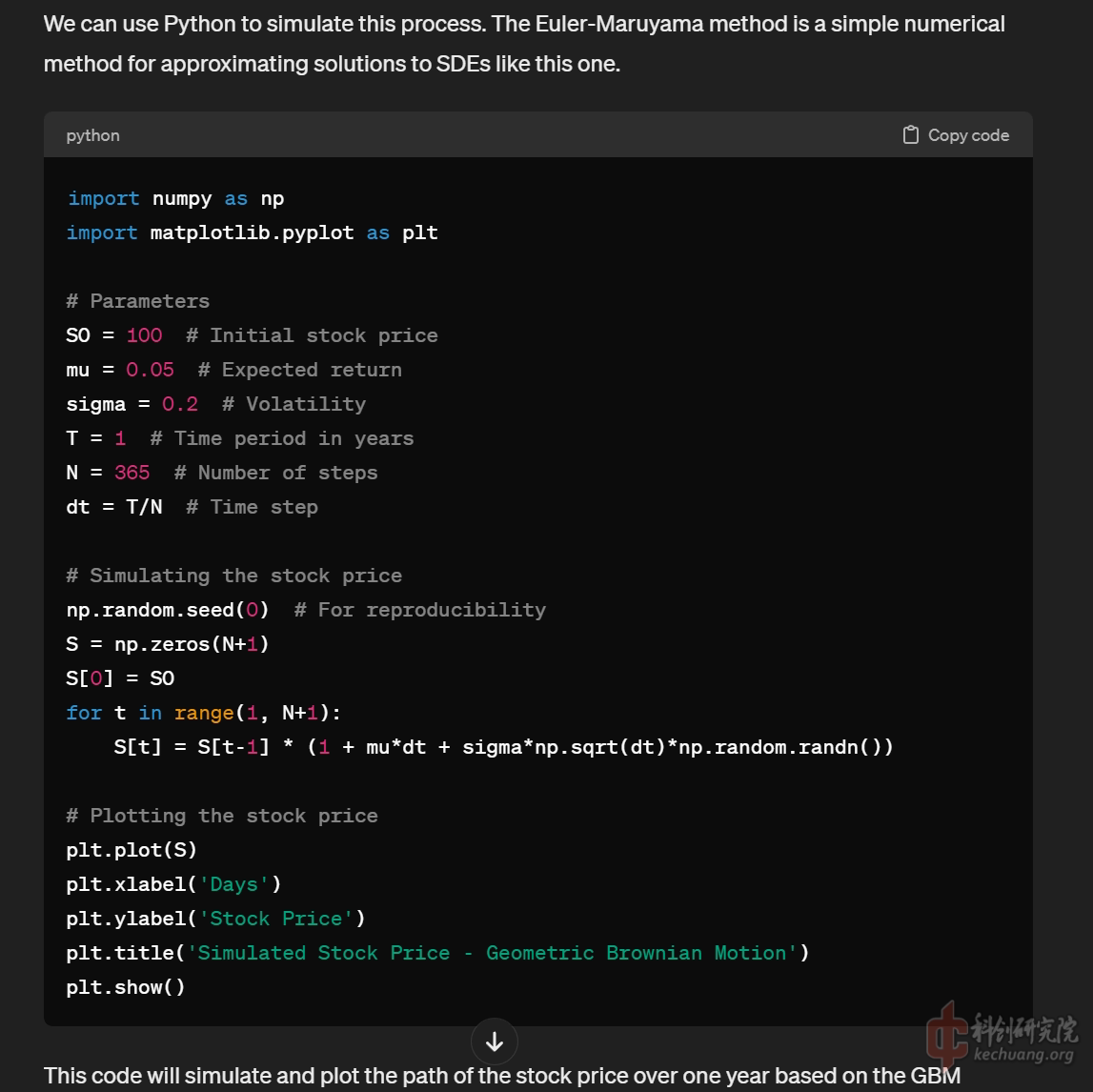
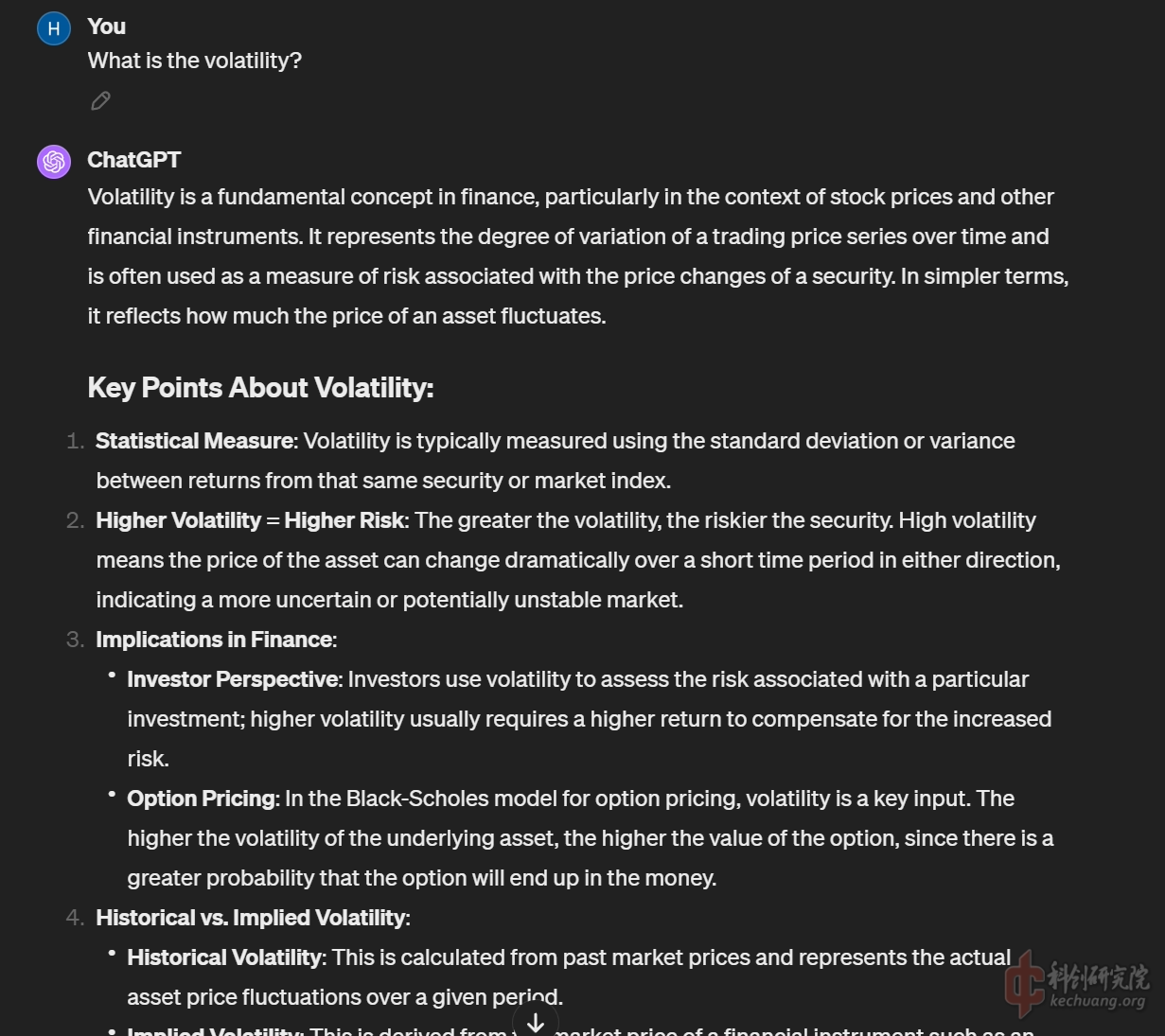
在给出了一个完全不需要纠错的简单模型程序后, 我进一步询问了其中涉及到的一些参数的具体市场意义的问题, GPT非但一一详细解答, 还进一步补充了这些参数可能可以如何通过历史数据获取的问题, 这让我那悬着担心自己需要长脑子才能学习这些知识的心终于可以放下了. 

还要求GPT帮忙添加了一些额外的图示功能, 显示随机微分方程中单纯对流项的直线, 以及由扩散项的随机参数在时间演化上的误差累积构成的正态分布区间. 

       值得注意的是, 本实例中的尝试, 首先通过吟唱术式:

'Please pretend to be a mathematician who is good at probability theory, especially stochastic differential equation, and also know about python programming and R studio programming. Answer me some questions in a step by step approach (I only know some simple calculus, no more than U.S. AP calculus).'

限定了AI生成内容的大范围, 以确保生成内容的专业性, 以及更加个性化根据个人实际情况出发的教学方式. 经实测相比起直接吟唱正式内容的咒语可以少走弯路. 

       除此以外, 热身后的正式内容(其实还有很多很多, 只是为了节省读者时间, 不作更多描述), 需要以由简入难, 由少至多的方式, 通过谨慎揣摩吟唱逻辑的方式, 缓慢堆砌, 因为实测中, 如果有语义模糊的吟唱, 很可能会导致GPT在生成一段'偏义'内容后, 导致整个法术结构崩溃. 通常这种情况笔者会抹除所有对话从头再来, 因为试图通过一系列进一步的术式限定来将主要内容拉回正轨, 往往其实会导致最终构成一个臃肿的弗兰肯斯坦式的怪物.