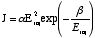第二部分 基本编程机制

无论是浮栅型或电荷阱型存储器，对器件编程都是通过将电子注入浮栅区或者氮层区中。实现此过程，主要是通过两种的机制：FN 隧道效应（对薄氧化层）以及热电子注入。

1． Fowler-Nordheim 隧道效应
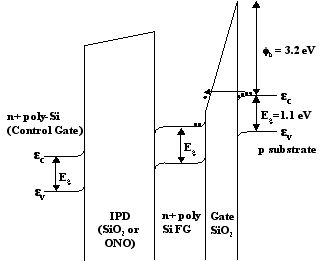
FN隧道效应是NVM最主要的电荷注入方式之一，在对器件编程时，在控制门极加上很大的电压（Vcg），能带结构会如图四变化：

在图四中，ec 和 ev 分别是导带和禁带，Eg 为能带宽度 (硅材料是1.1 eV ), fb 为Si-SiO2 能量势垒 (fb is 3.2 eV for electrons and 4.7 eV for holes). 外加电压 Vcg 造成电势提供给substrate中的电子通过薄氧化层中的隧道到达浮栅区的可能。弯曲的IPD和门氧化层能带是不同的，这是由于它们的厚度不同。IPD厚度从25nm到45nm不等，而门氧化层厚度只有5nm到12nm。电子到达浮栅区而形成的电流密度为：



其中,
h = 普朗克常数
= 诸如表面能量势垒 (3.2 eV for Si-SiO2)
q = 单个电子电量 (1.6x10-19 C)
m = 自由电子质量 (9.1x10-31 kg)
m* = 二氧化硅能带中自由电子有效质量 (0.42 m)
Vinj = 注入表面电势
Vapp = 门氧化层两侧电势 (V)
Vfb = 平带电势(V)
tox = 门氧化层厚度 (cm)

等式 1 隧道电流密度和加在门氧化层两侧电势Vapp成指数比， 从而影响诸如表面电势Vinj。图五展示了一个NVM的横截面，其电子隧道效应电流成均匀分布。Vcg 正电压，源极Vs 和漏极 Vd, 以及substrate Vsub 都接地。

另一个可选的对FLASH编程的方法如图六所示，被称为漏极隧道效应。此方法有时比均匀隧道效应编程在编程速度方面更有利，由于注入面积很小，产生的隧道电流密度更大。