非线性是可以校准的 校准是磁编的一个问题 不能买来就用 如果是磁编直接当光编使用 沿用以往的算法 肯定不行啊 厂家手册里面都给出了非线性度 但是那都是轴对得非常准得情况 而且抖动的另一个可能是时间误差 光编几乎是立即响应 磁编里面需要采样时间 有滤波等计算 就会出现线性系统遇到容性滞后没有超前补偿的不稳定状态 实际上 开源的闭环驱动算法里面都有这个超前角补偿的 (有意思的是 我看到一段开源代码 直言这个地方是抄的 只知道用起来好 有种"屎山勿移 易崩塌"的感觉)

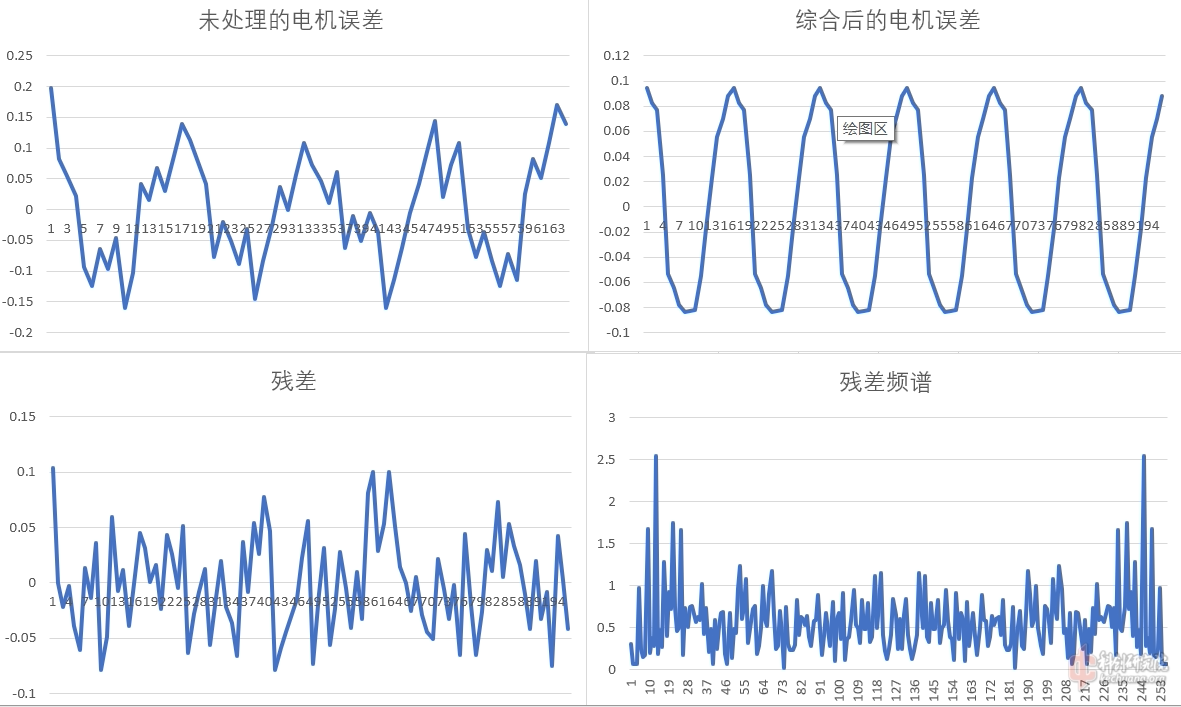
前面计算的电机误差看起来有点复杂(左上图) 但是其实是重复的 而且数据中充满了因为磁编的量化误差 所以我把它进行了分组平均 每个数据和所有增加1.8度的整数倍的数据平均  因为16细分 所以得到16点平均后的数据 (右上图) 看起来齿槽转矩的样子就准确多了  这是最终用来校正开环电流的数据 (实际上 处理完数据后 我才觉得 似乎用64点间隔 整个单极的一圈 才对 不过基本相差不大)

剩下的残差和其频谱(左下右下图) 表示 基本洗白了 没法处理了 但是从量级而言 只是比齿槽转矩误差略小 这大概就是系统精度能达到的最理想情况 与磁编量化级带来的误差接近 这大概是主要出于此了