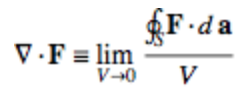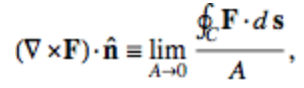简单总结：
电荷产生电场（高斯），不存在磁单极子（高斯磁）
电流产生磁场，变化的电场也可以产生磁场（麦克斯韦-安培），变化的磁场也可以产生电场（法拉第）
—————————————————————————————————————————————————————————
电磁场是矢量场，可以粗略认为空间中每个点都对应一个矢量，指出了这点的电场/磁场的方向与大小。
就像这样：

电场散度的意义粗糙的理解是，在一个点“附近”射出电场线数目与射入电场线数目的差。
就是一个矢量在一个闭区域内，其单位体积内通量的大小，通量即是通过之量的意思。

理解散度，先要理解通量（是一种闭合曲面积分）。

矢量的通量即是这个矢量对X,Y,Z的偏导的和（标量），通量通俗的讲正可以理解为一个矢量在一个曲面的累积效果（穿过的“电场线数目”），就像积分的本质就是求和一样。
可以在这个点附近做一球，将所有“净”射出球内的矢量在球面法线的投影叠加（即“通量”），令球的半径不断缩小，这个叠加值就是这一点电场的散度。
运算的对象是向量,运算出来的结果会是标量，就像穿过的“电场线数目”是一个数。
（闭合曲面上每一点都对应有一个矢量，就是这个点上的“电场强度”，如果这个电场强度的方向指向是垂直于这个面的，它在这一点曲面法线方向的投影就大，它对通量的贡献就大）
仅作理解，如果现在我们考虑任何一个点(或者说这个点的周围极小的一块区域),在这个点上,向量场的发散程度,如果是正的,代表这些向量场是往外散出的.如果是负的,代表这些向量场是往内集中的.

散度的一个 定义：


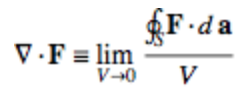
其中的曲面积分就可理解为通量。散度就是“ 通量” 在闭合曲面（可以理解为球面）体积不断不断缩小，无限趋近一个点时的极限

高斯公式：
矢量穿过任意闭合曲面的通量等于矢量的散度对闭合面所包围的体积的积分。

可以理解为：

散度是一颗一颗的，你想知道封闭房间的天花板墙壁和地板上总共照了多少光（光通量，闭合曲面积分），只需要数一下房间里亮了多少颗灯泡（可以理解为散度的体积分，灯泡，不就是一个光最发散的地方吗，积分就是求和，所以要把所有灯泡都加起来就行。

现在来理解 高斯磁定律 与 高斯定律（参看表格）

高斯磁定律：
微分形式：磁感应强度的散度为0，即为这个磁场是无源可寻的，这也就说明无法寻找到磁单极。在任何地方都找不到“发散源”
对微分形式两边在一闭合S面上积分，就得到积分形式。这样我们在磁场中任做一闭合曲面，对磁场做曲面积分，得到的结果一定是 0，应为穿进来的磁场线一定会穿出去，一一抵消。

高斯定律：
揭示了电场是一个有源场，什么是有源场呢？？该场的散度是由实体物质（正负电子）所“发出”，是有源可寻的。
积分形式：在电场中任做一闭合曲面，要求出电通量，只用将包围其中的电荷（源）叠加即可
微分形式：通量的极限是散度，所以两边取极限，不难想象，左边应该是电场的散度，右边则是一个无限小区域内的电荷数目，其实就是电荷的“密度”


接下来是旋度：

（等式两边都是标量，仅是旋度的大小，因为方向可简单由右手螺旋定则得到）

理解旋度，先要理解环量（是一种回路积分）。

矢量场的环量，实际上就是这个矢量场在一个场中的“闭合曲线（C）”上沿曲线切线方向的积累（闭合曲线上每一点都对应有一个矢量，就是这个点上的“电场强度”，如果这个电场强度的方向指向是顺着曲线的，它在这一点曲线切线方向的投影就大，它对环量的贡献就大）。
这就是环量，环量越大，说明这个矢量在闭合曲线上的积累越多。

投影的叠加，运算结果是一个矢量，为什么呢？因为这个”积累“有方向。但是这个方向只与环绕方向（沿曲线积分的方向）有关，因此只有两种情况，顺时针、逆时针。所以就自然而然的规定该方向与曲线的环绕方向满足右手螺旋定则，即此曲线围绕面的法线方向——要么垂直向上要么垂直向下
现在让这个”环“的面积 A 不断缩小，可以理解为一个半径不断减小的圆，最终会小到几乎看起来是一个点。这个环量的极限就是旋度。

很容易明白，对于静电场而言，其电场强度的旋度为0，因为在静电场中任找一个闭合回路，总电势（在回路上的每一个线微元δ上ΔU=E‘δ，E‘即电场沿δ切线的投影，求和即可。微元的求和，也就是积分）一定为零，所以这个环量（电势）的极限——旋度，也是0。而对于感应电场，磁通量的变化率决定了一个回路中感应电压的大小，对应到电场就是所谓涡旋电场，这就是法拉第电磁感应定律，对回路取极限容易得到其微分形式。
而对于磁场，在稳恒电流下，由毕奥萨伐定律可以得到一小截通电导线（电流元）周围的磁场分布，进而得到长直导线周围的磁场分布，由此可以得到安培环路定理。即：磁场的环量正比于穿过此环路的净电流和。而环量取极限得到旋度，电流对截面大小取极限就是电流密度矢量。


进一步理解，再考虑这里的”电流“，即电流密度矢量在电荷通过截面上的（其实不一定有电荷通过，可以先这么理解）曲面积分。对于稳恒电流，电流大小就是单位时间内通过导线截面的电荷总量；微观上说，就是电流密度矢量在导线截面的通量。由于电荷不能凭空产生，任取一固定的闭合曲面，进入和出去的电荷量一定相同，否则导线的某个地方的电荷会越来越多或越来越少，都是不可能的；这就是说，对于稳恒电流，电流密度矢量在闭合曲面的通量为0.而对于非稳恒情况，例如电容器放电，对只包围其中一个极板的闭合曲面，电流密度矢量的通量可以不是0，宏观上看就是只有电流流出没有电流流入。所以麦克斯韦引入所谓位移电流来解释这一部分的非稳恒电流，这样引入位移电流的总电流密度矢量的通量依旧是0.至于位移电流的组成,可分为电场强度的随时间变化率（真空中也存在）与介质的极化强度随时间变化率。这样，麦克斯韦-安培定律右边就有两项（其中的总电流I包括稳恒部分（电荷移动）以及位移电流中的介质的极化强度随时间变化率的部分）

参考文献：
XXXXXXXXXXXXXXXXXXXX/question/25121612
XXXXXXXXXXXXXXXXXXXX/question/21912411
XXXXXXXXXXXXXXXXXXXXXXX/s/blog_XXXXXXXXXXXXXXXXXXXml